Τελευταία αναθεώρηση της 15:10, 15 Νοεμβρίου 2020

Μαθηματικές σταθερές

$π = σ υ ν^{- 1} (\begin{matrix} - 1 \end{matrix}) ≃ 3, 141592653589793238462643 . . .$

$e = \lim_{n \to \infty} {(\begin{matrix} 1 + \frac{1}{n} \end{matrix})}^{n} ≃ 2, 718281828459045235360287 . . .$

e: βάση των φυσικών λογαρίθμων.

$\sqrt{2} = 2^{\frac{1}{2}} ≃ 1, 4142135623730950488 . . .$

$\sqrt{3} = 3^{\frac{1}{2}} ≃ 1, 7320508075688772935 . . .$

$\sqrt{5} = 5^{\frac{1}{2}} ≃ 2, 2360679774997896964 . . .$

$\sqrt[3]{2} = 2^{\frac{1}{3}} ≃ 1, 259921050 . . .$

$\sqrt[3]{3} = 3^{\frac{1}{3}} ≃ 1, 442249570 . . .$

$\sqrt[5]{2} = 2^{\frac{1}{5}} ≃ 1, 148698355 . . .$

$\sqrt[5]{3} = 3^{\frac{1}{5}} ≃ 1, 245730940 . . .$

$e^{π} ≃ 23, 140692632779269006 . . .$

$π^{e} ≃ 22, 45915771836104547342715 . . .$

$e^{e} ≃ 15, 154262241479264190 . . .$

$l o g_{10} 2 = \frac{l n 2}{l n 10} ≃ 0, 3010299956639811952137389 . . .$

$l o g_{10} 3 = \frac{l n 3}{l n 10} ≃ 0, 4771212547196624372950279 . . .$

$l o g_{10} e = \frac{l n e}{l n 10} = \frac{1}{l n 10} ≃ 0, 43429448190325182765 . . .$

$l o g_{10} π = \frac{l n π}{l n 10} ≃ 0, 4971498726941338543512683 . . .$

$l n 10 ≃ 2, 302585092994045684017991 . . .$

$l n 2 ≃ 0, 693147180559945309417232 . . .$

$l n 3 ≃ 1, 098612288668109691395245 . . .$

$γ = \lim_{n \to \infty} (\begin{matrix} \begin{matrix} n \\ \sum \\ i = 1 \end{matrix} \frac{1}{n} - l n n \end{matrix}) ≃ 0, 577215664901532860606512 . . .$

γ: σταθερά Euler.

$e^{γ} ≃ 1, 7810724179901979852 . . .$

$\sqrt{e} = e^{\frac{1}{2}} ≃ 1, 6487212707001281468 . . .$

$\sqrt{π} = π^{\frac{1}{2}} = Γ (\begin{matrix} \frac{1}{2} \end{matrix}) ≃ 1, 772453850905516027298167 . . .$

Γ: Συνάρτηση Γ.

$Γ (\begin{matrix} \frac{1}{3} \end{matrix}) ≃ 2, 678938534707748 . . .$

$Γ (\begin{matrix} \frac{1}{4} \end{matrix}) ≃ 3, 625609908221908 . . .$

$1 r a d = \frac{18 0^{o}}{π} ≃ 57, 29577951308232 . . .^{o}$

rad = ακτίνιο.

$1^{o} = \frac{π}{180} r a d ≃ 0, 0174532925199432957 . . . r a d$

Αξιοσημείωτες ταυτότητες

Αναπτύγματα δυνάμεων διωνύμων

Οι επόμενοι τύποι αποτελούν μερική εφαρμογή του τύπου διωνύμου για $2 \leq n \leq 6$ .

${(\begin{matrix} α + β \end{matrix})}^{2} = α^{2} + 2 α β + β^{2}$

Ανάπτυγμα τετραγώνου αθροίσματος δύο όρων.

${(\begin{matrix} α - β \end{matrix})}^{2} = α^{2} - 2 α β + β^{2}$

Ανάπτυγμα τετραγώνου διαφοράς δύο όρων.

${(\begin{matrix} α + β \end{matrix})}^{3} = α^{3} + 3 α^{2} β + 3 α β^{2} + β^{3}$

Ανάπτυγμα κύβου αθροίσματος δύο όρων.

${(\begin{matrix} α - β \end{matrix})}^{3} = α^{3} - 3 α^{2} β + 3 α β^{2} - β^{3}$

Ανάπτυγμα κύβου διαφοράς δύο όρων.

${(\begin{matrix} α + β \end{matrix})}^{4} = α^{4} + 4 α^{3} β + 6 α^{2} β^{2} + 4 α β^{3} + β^{4}$

Ανάπτυγμα τέταρτης δύναμης αθροίσματος δύο όρων.

${(\begin{matrix} α - β \end{matrix})}^{4} = α^{4} - 4 α^{3} β + 6 α^{2} β^{2} - 4 α β^{3} + β^{4}$

Ανάπτυγμα τέταρτης δύναμης διαφοράς δύο όρων.

${(\begin{matrix} α + β \end{matrix})}^{5} = α^{5} + 5 α^{4} β + 10 α^{3} β^{2} + 10 α^{2} β^{3} + 5 α β^{4} + β^{5}$

Ανάπτυγμα πέμπτης δύναμης αθροίσματος δύο όρων.

${(\begin{matrix} α - β \end{matrix})}^{5} = α^{5} - 5 α^{4} β + 10 α^{3} β^{2} - 10 α^{2} β^{3} + 5 α β^{4} - β^{5}$

Ανάπτυγμα πέμπτης δύναμης διαφοράς δύο όρων.

${(\begin{matrix} α + β \end{matrix})}^{6} = α^{6} + 6 α^{5} β + 15 α^{4} β^{2} + 20 α^{3} β^{3} + 15 α^{2} β^{4} + 6 α β^{5} + β^{6}$

Ανάπτυγμα έκτης δύναμης αθροίσματος δύο όρων.

${(\begin{matrix} α - β \end{matrix})}^{6} = α^{6} - 6 α^{5} β + 15 α^{4} β^{2} - 20 α^{3} β^{3} + 15 α^{2} β^{4} - 6 α β^{5} + β^{6}$

Ανάπτυγμα έκτης δύναμης διαφοράς δύο όρων.

Οι συντελεστές μπορούν να υπολογιστούν από το τρίγωνο του Πασκάλ. Στην παραπάνω εικόνα η δύναμη είναι στην αριστερή στήλη, ενώ οι αντίστοιχοι συντελεστές βρίσκονται στην ίδια γραμμή και στη σειρά συνήθης ανάπτυξης του διωνύμου.

Παραγοντοποιήσεις

Παραγοντοποιήσεις αθροισμάτων και διαφορών δυνάμεων

$α^{2} - β^{2} = (\begin{matrix} α + β \end{matrix}) (\begin{matrix} α - β \end{matrix})$

Παραγοντοποίηση διαφοράς τετραγώνων.

$α^{3} - β^{3} = (\begin{matrix} α - β \end{matrix}) (\begin{matrix} α^{2} + α β + β^{2} \end{matrix})$

Παραγοντοποίηση διαφοράς κύβων.

$α^{3} + β^{3} = (\begin{matrix} α + β \end{matrix}) (\begin{matrix} α^{2} - α β + β^{2} \end{matrix})$

Παραγοντοποίηση αθροίσματος κύβων.

$α^{4} - β^{4} = (\begin{matrix} α - β \end{matrix}) (\begin{matrix} α + β \end{matrix}) (\begin{matrix} α^{2} + β^{2} \end{matrix})$

Παραγοντοποίηση διαφοράς τέταρτης δύναμης.

$α^{5} - β^{5} = (\begin{matrix} α - β \end{matrix}) (\begin{matrix} α^{4} + α^{3} β + α^{2} β^{2} + α β^{3} + β^{4} \end{matrix})$

Παραγοντοποίηση διαφοράς πέμπτης δύναμης.

$α^{5} + β^{5} = (\begin{matrix} α + β \end{matrix}) (\begin{matrix} α^{4} - α^{3} β + α^{2} β^{2} - α β^{3} + β^{4} \end{matrix})$

Παραγοντοποίηση αθροίσματος πέμπτης δύναμης.

$α^{6} - β^{6} = (\begin{matrix} α - β \end{matrix}) (\begin{matrix} α + β \end{matrix}) (\begin{matrix} α^{2} + α β + β^{2} \end{matrix}) (\begin{matrix} α^{2} - α β + β^{2} \end{matrix})$

Παραγοντοποίηση διαφοράς έκτης δύναμης.

Γενίκευση παραγοντοποιήσεων αθροισμάτων και διαφορών δυνάμεων

Οι παρακάτω τύποι ισχύουν για $n \in ℕ^{*} = ℕ - {\begin{matrix} 0 \end{matrix}}$

$α^{2 n + 1} - β^{2 n + 1} = (\begin{matrix} α - β \end{matrix}) \sum_{i = 0}^{2 n} α^{2 n - i} β^{i} = (\begin{matrix} α - β \end{matrix}) \prod_{i = 1}^{n} (\begin{matrix} α^{2} - 2 α β σ υ ν \frac{2 i π}{2 n + 1} + β^{2} \end{matrix})$

$α^{2 n + 1} + β^{2 n + 1} = (\begin{matrix} α + β \end{matrix}) \sum_{i = 0}^{2 n} (- 1)^{i} α^{2 n - i} β^{i} = (\begin{matrix} α + β \end{matrix}) \prod_{i = 1}^{n} (\begin{matrix} α^{2} + 2 α β σ υ ν \frac{2 i π}{2 n + 1} + β^{2} \end{matrix})$

$α^{2 n} - β^{2 n} = (\begin{matrix} α + β \end{matrix}) (\begin{matrix} α - β \end{matrix}) \sum_{i = 0}^{n} α^{n - 1 - i} β^{i} \sum_{i = 0}^{n} (- 1)^{i} α^{n - 1 - i} β^{i} = (\begin{matrix} α + β \end{matrix}) (\begin{matrix} α - β \end{matrix}) \prod_{i = 1}^{n - 1} (\begin{matrix} α^{2} - 2 α β σ υ ν \frac{i π}{n} + β^{2} \end{matrix})$

$α^{2 n} + β^{2 n} = \prod_{i = 1}^{n} (\begin{matrix} α^{2} + 2 α β σ υ ν \frac{(\begin{matrix} 2 i - 1 \end{matrix}) π}{2 n} + β^{2} \end{matrix})$

Άλλες παραγοντοποιήσεις

$α^{4} + α^{2} β^{2} + β^{4} = (\begin{matrix} α^{2} + α β + β^{2} \end{matrix}) (\begin{matrix} α^{2} - α β + β^{2} \end{matrix})$

$α^{4} + 4 β^{4} = (\begin{matrix} α^{2} + 2 α β + 2 β^{2} \end{matrix}) (\begin{matrix} α^{2} - 2 α β + 2 β^{2} \end{matrix})$

Ο τύπος του Διωνύμου και οι Διωνυμικοί Συντελεστές

Το παραγοντικό

Για $n \in ℕ^{*} = ℕ - {\begin{matrix} 0 \end{matrix}}$ ορίζεται:

$n! = \prod_{i = 1}^{n} i$ .

Για n = 0 ορίζεται:

$0! = 1$ .

Ο τύπος του διωνύμου

Για $n \in ℕ^{*} = ℕ - {\begin{matrix} 0 \end{matrix}}$ είναι:

${(\begin{matrix} α + β \end{matrix})}^{n} = α^{n} + \sum_{i = 1}^{n} \frac{n!}{i! (\begin{matrix} n - i \end{matrix})!} α^{n - i} β^{i}$

Διωνυμικοί συντελεστές

Για $n \in ℕ^{*} = ℕ - {\begin{matrix} 0 \end{matrix}}$ και $\forall i \in {\begin{matrix} 1, 2, 3 . . . n \end{matrix}} \subset ℕ^{*}$ ορίζονται οι διωνυμικοί συντελεστές ως εξής:

$(\binom{n}{i}) = \frac{n!}{i! (\begin{matrix} n - i \end{matrix})!} = (\binom{n}{n - i})$

Ακόμη ορίζεται:

$(\binom{n}{0}) = 1$

Ιδιότητες των διωνυμικών συντελεστών

$(\binom{n}{i}) + (\binom{n}{i + 1}) = (\binom{n + 1}{i + 1})$

Η σχέση δίνει το τρίγωνο του Pascal.

$\sum_{i = 0}^{n} (\binom{n}{i}) = 2^{n}$

$\sum_{i = 0}^{n} {(\begin{matrix} - 1 \end{matrix})}^{i} (\binom{n}{i}) = 0$

$\sum_{i = 0}^{m} (\binom{n + i}{n}) = (\binom{n + m + 1}{n + 1}), m \in ℕ$

$\sum_{i = 0}^{k} (\binom{n}{2 i}) = 2^{n - 1}, k = [\begin{matrix} \frac{n}{2} \end{matrix}]$

$\sum_{i = 0}^{k} (\binom{n}{2 i + 1}) = 2^{n - 1}, k = [\begin{matrix} \frac{n - 1}{2} \end{matrix}]$

$\sum_{i = 0}^{n} {(\binom{n}{i})}^{2} = (\binom{2 n}{n})$

$\sum_{i = 0}^{p} (\binom{m}{i}) (\binom{n}{p - i}) = (\binom{m + n}{p}), m \in ℕ, p \leq m i n {\begin{matrix} m, n \end{matrix}} \land p \in ℕ$

$\sum_{i = 1}^{n} i (\binom{n}{i}) = n 2^{n - 1}$

$\sum_{i = 1}^{n} {(\begin{matrix} - 1 \end{matrix})}^{i + 1} i (\binom{n}{i}) = 0$

Επέκταση για δυνάμεις πολυωνύμων

${(\begin{matrix} \begin{matrix} p \\ \sum \\ i = 1 \end{matrix} α_{i} \end{matrix})}^{n} = \sum_{i = 1}^{p} \frac{n!}{\begin{matrix} p \\ \prod \\ i = 1 \end{matrix} n_{i}!} \prod_{i = 1}^{p} α_{i}^{n_{i}}, p \in ℕ^{*}, n_{i} \in ℕ^{*} \land \sum_{i = 1}^{p} n_{i} = n$

Τύποι Κλασικής Γεωμετρίας

Γεωμετρικά σχήματα

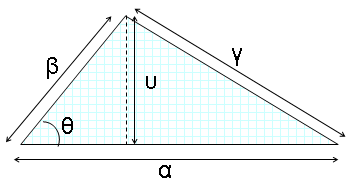
Τρίγωνο

Περίμετρος:

$Π = α + β + γ$

Εμβαδό:

$E = \frac{α υ}{2} = \frac{α β η μ θ}{2} = \sqrt{s (s - α) (s - β) (s - γ)}$ , όπου $s = \frac{Π}{2} = \frac{α + β + γ}{2}$ (ημιπερίμετρος)

Στην περίπτωση ορθογωνίου τριγώνου είναι $θ = 9 0^{o} \Rightarrow η μ θ = 1$ . Άρα: β = υ και:

$E = \frac{α β}{2}$ .

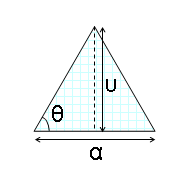
Στην περίπτωση ισόπλευρου τριγώνου είναι: $α = β = γ$ , $θ = 6 0^{o}$ και $s = \frac{3}{2} α$ . Οπότε:

Περίμετρος:

$Π = 3 α$

Εμβαδό:

$E = \frac{α υ}{2} = \frac{α^{2} η μ 6 0^{o}}{2} = \frac{\sqrt{3}}{4} α^{2}$

Το ίδιο προκύπτει και από τον άλλο τύπο:

$E = \sqrt{\frac{3}{2} α {(\begin{matrix} \frac{3}{2} α - α \end{matrix})}^{3}} = \sqrt{\frac{3}{2} α {(\begin{matrix} \frac{1}{2} α \end{matrix})}^{3}} = \sqrt{\frac{3 α^{4}}{2^{4}}} = \frac{\sqrt{3}}{4} α^{2}$

Ορθογώνιο παραλληλόγραμμο

Περίμετρος:

$Π = 2 (α + β)$

Εμβαδό:

$E = α β$

Πλάγιο παραλληλόγραμμο

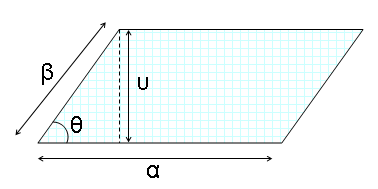
Περίμετρος:

$Π = 2 (α + β)$

Εμβαδό:

$E = β υ = α β η μ θ$

Ρόμβος

Περίμετρος:

$Π = 4 α$

Εμβαδό:

$E = \frac{δ_{1} δ_{2}}{2}$

Τετράγωνο

Περίμετρος:

$Π = 4 α$

Εμβαδό:

$E = α^{2}$

Τραπέζιο

Περίμετρος:

$Π = α + β + (\frac{1}{s i n θ} + \frac{1}{s i n ϕ}) υ$

Εμβαδό:

$E = \frac{α + β}{2} υ$

Κανονικό πολύγωνο

1. Κανονικό πολύγωνο με n πλευρές και πλευρά α

Περίμετρος:

$Π = n α$

Εμβαδό:

$E = \frac{1}{4} n α^{2} c o t \frac{π}{n} = \frac{1}{4} n α^{2} \frac{σ υ ν \frac{π}{n}}{η μ \frac{π}{n}}$

2. Κανονικό πολύγωνο με n πλευρές εγγεγραμμένο σε κύκλο ακτίνας r

Περίμετρος:

$Π = 2 n r s i n \frac{π}{n}$

Εμβαδό:

$E = \frac{1}{2} n r^{2} \sin \frac{2 π}{n}$

3. Κανονικό πολύγωνο με n πλευρές περιγεγραμμένο σε κύκλο ακτίνας r

Περίμετρος:

$Π = 2 n r t a n \frac{π}{n}$

Εμβαδό:

$E = \frac{1}{2} n r^{2} t a n \frac{2 π}{n}$

Κύκλος

1. Κύκλος με ακτίνα r:

Περιφέρεια:

$Π = 2 π r$

Εμβαδό:

$E = π r^{2}$

2. Τομέας κύκλου ακτίνας r, τόξου θ (σε ακτίνια, rad):

Μήκος τόξου:

$Π = r θ$

Εμβαδό:

$E = \frac{1}{2} r^{2} θ$

3. Τμήμα κύκλου ακτίνας r, τόξου θ (σε ακτίνια, rad):

$E = \frac{1}{2} r^{2} (θ - s i n θ)$

4. Κύκλος ακτίνας r εγγεγραμμένος σε τρίγωνο με πλευρές α, β, γ:

$r = \frac{\sqrt{s (s - α) (s - β) (s - γ)}}{s}$
όπου $s = \frac{Π}{2} = \frac{1}{2} (α + β + γ)$

5. Κύκλος ακτίνας r περιγεγραμμένος σε τρίγωνο με πλευρές α, β, γ:

$r = \frac{α β γ}{4 \sqrt{s (s - α) (s - β) (s - γ)}}$
όπου $s = \frac{Π}{2} = \frac{1}{2} (α + β + γ)$

Τριγωνομετρικοί τύποι

Ημίτονο της Β:

$s i n B = η μ B = \frac{y}{r}$

Συνημίτονο της Β:

$c o s B = σ υ ν B = \frac{x}{r}$

Εφαπτομένη της Β:

$t a n B = ϵ ϕ B = \frac{y}{x}$

Συνεφαπτομένη της Β:

$c o t B = σ ϕ B = \frac{x}{y}$

Τέμνουσα της Β:

$s e c B = \frac{r}{x}$

Συντέμνουσα της Β:

$c s c B = \frac{r}{y}$

Σχέσεις μεταξύ τριγωνομετρικών αριθμών

$t a n B = \frac{s i n B}{c o s B}$

$c o t B = \frac{1}{t a n B} = \frac{c o s B}{s i n B}$

$s e c B = \frac{1}{c o s B}$

$c s c B = \frac{1}{s i n B}$

$s i n^{2} B + c o s^{2} B = 1$

$s e c^{2} B - t a n^{2} B = 1$

$c s c^{2} B - c o t^{2} B = 1$

Τιμές των τριγωνομετρικών συναρτήσεων διαφόρων γωνιών

Β (°)	Β (rad)	sin B	cos B	tan B	cot B	sec B	csc B
0	0	0	1	0	±∞	1	±∞
15	$\frac{π}{12}$	$\frac{1}{4} (\sqrt{6} - \sqrt{2})$	$\frac{1}{4} (\sqrt{6} + \sqrt{2})$	$2 - \sqrt{3}$	$2 + \sqrt{3}$	$\sqrt{6} - \sqrt{2}$	$\sqrt{6} + \sqrt{2}$
30	$\frac{π}{6}$	$\frac{1}{2}$	$\frac{1}{2} \sqrt{3}$	$\frac{1}{3} \sqrt{3}$	$\sqrt{3}$	$\frac{2}{3} \sqrt{3}$	2
45	$\frac{π}{4}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2} \sqrt{2}$	1	1	$\sqrt{2}$	$\sqrt{2}$
60	$\frac{π}{3}$	$\frac{1}{2} \sqrt{3}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{1}{3} \sqrt{3}$	2	$\frac{2}{3} \sqrt{3}$
75	$\frac{5 π}{12}$	$\frac{1}{4} (\sqrt{6} + \sqrt{2})$	$\frac{1}{4} (\sqrt{6} - \sqrt{2})$	$2 + \sqrt{3}$	$2 - \sqrt{3}$	$\sqrt{6} + \sqrt{2}$	$\sqrt{6} - \sqrt{2}$
90	$\frac{π}{2}$	1	0	±∞	0	±∞	1
105	$\frac{7 π}{12}$	$\frac{1}{4} (\sqrt{6} + \sqrt{2})$	$- \frac{1}{4} (\sqrt{6} - \sqrt{2})$	$- (2 + \sqrt{3})$	$- (2 - \sqrt{3})$	$- (\sqrt{6} + \sqrt{2})$	$\sqrt{6} - \sqrt{2}$
120	$\frac{2 π}{3}$	$\frac{1}{2} \sqrt{3}$	$- \frac{1}{2}$	$- \sqrt{3}$	$- \frac{1}{3} \sqrt{3}$	-2	$\frac{2}{3} \sqrt{3}$
135	$\frac{3 π}{4}$	$\frac{1}{2} \sqrt{2}$	$- \frac{1}{2} \sqrt{2}$	-1	-1	$- \sqrt{2}$	$\sqrt{2}$
150	$\frac{5 π}{6}$	$\frac{1}{2}$	$- \frac{1}{2} \sqrt{3}$	$- \frac{1}{3} \sqrt{3}$	$- \sqrt{3}$	$- \frac{2}{3} \sqrt{3}$	2
165	$\frac{11 π}{12}$	$\frac{1}{4} (\sqrt{6} - \sqrt{2})$	$- \frac{1}{4} (\sqrt{6} + \sqrt{2})$	$2 - \sqrt{3}$	$- (2 + \sqrt{3})$	$- (\sqrt{6} - \sqrt{2})$	$\sqrt{6} + \sqrt{2}$
180	π	0	-1	0	$\mp \infty$	-1	±∞
195	$\frac{13 π}{12}$	$- \frac{1}{4} (\sqrt{6} - \sqrt{2})$	$- \frac{1}{4} (\sqrt{6} + \sqrt{2})$	$2 - \sqrt{3}$	$2 + \sqrt{3}$	$- (\sqrt{6} - \sqrt{2})$	$- (\sqrt{6} + \sqrt{2})$
210	$\frac{7 π}{6}$	$- \frac{1}{2}$	$- \frac{1}{2} \sqrt{3}$	$\frac{1}{3} \sqrt{3}$	$- \sqrt{3}$	$- \frac{2}{3} \sqrt{3}$	-2
225	$\frac{5 π}{4}$	$- \frac{1}{2} \sqrt{2}$	$- \frac{1}{2} \sqrt{2}$	1	1	$- \sqrt{2}$	$- \sqrt{2}$
240	$\frac{4 π}{3}$	$- \frac{1}{2} \sqrt{3}$	$- \frac{1}{2}$	$\sqrt{3}$	$\frac{1}{3} \sqrt{3}$	-2	$- \frac{2}{3} \sqrt{3}$
255	$\frac{17 π}{12}$	$- \frac{1}{4} (\sqrt{6} + \sqrt{2})$	$- \frac{1}{4} (\sqrt{6} - \sqrt{2})$	$2 + \sqrt{3}$	$2 - \sqrt{3}$	$- (\sqrt{6} + \sqrt{2})$	$- (\sqrt{6} - \sqrt{2})$
270	$\frac{3 π}{2}$	-1	0	±∞	0	$\mp \infty$	-1
285	$- \frac{17 π}{12}$	$\frac{1}{4} (\sqrt{6} + \sqrt{2})$	$- \frac{1}{4} (\sqrt{6} - \sqrt{2})$	$- (2 + \sqrt{3})$	$- (2 - \sqrt{3})$	$\sqrt{6} + \sqrt{2}$	$- (\sqrt{6} - \sqrt{2})$
300	$\frac{5 π}{3}$	$- \frac{1}{2} \sqrt{3}$	$\frac{1}{2}$	$- \sqrt{3}$	$- \frac{1}{3} \sqrt{3}$	2	$- \frac{2}{3} \sqrt{3}$
315	$\frac{7 π}{4}$	$- \frac{1}{2} \sqrt{2}$	$\frac{1}{2} \sqrt{2}$	-1	-1	$\sqrt{2}$	$- \sqrt{2}$
330	$\frac{11 π}{6}$	$- \frac{1}{2}$	$- \frac{1}{2} \sqrt{3}$	$- \frac{1}{3} \sqrt{3}$	$\sqrt{3}$	$- \frac{2}{3} \sqrt{3}$	-2
345	$\frac{23 π}{12}$	$- \frac{1}{4} (\sqrt{6} - \sqrt{2})$	$\frac{1}{4} (\sqrt{6} + \sqrt{2})$	$- (2 - \sqrt{3})$	$- (2 + \sqrt{3})$	$\sqrt{6} - \sqrt{2}$	$- (\sqrt{6} + \sqrt{2})$
360	2π	0	1	0	$\mp \infty$	1	$\mp \infty$

Τύποι αναλυτικής γεωμετρίας

Όλες οι γεωμετρικές σχέσεις μπορούν να περιγραφούν με διανυσματικές σχέσεις. Το τυπολόγιο αυτό στηρίζεται στις πράξεις μεταξύ διανυσμάτων.

Βασικές σχέσεις

δ=αx+βy+γz κατά μοναδικό τρόπο
δ γ=προβ_γδ γ
άρα δ γ=0 <=> δ και γ κάθετα μεταξύ τους
det|δ,γ|=|δxγ| είναι κατά απόλυτη τιμή το εμβαδόν του πλάγιου παραλληλόγραμμου που ορίζουν τα διανύσματα δ και γ
άρα det|δ,γ|=|δxγ|=0 <=> δ//γ <=> υπάρχει πραγματικός λ τέτοιος, ώστε γ=λδ
|δ|²=α²+β²+γ²
|δ| δεν είναι αρνητικός

Πράξεις με το συν-πλην άπειρο

Το συν άπειρο μπορεί να διανοηθεί ως ο μεγαλύτερος δυνατός αριθμός, ή για την ακρίβεια ως άπειρο εκλαμβάνουμε συνήθως ένα μέγεθος που τείνει στο συν ή πλην άπειρο. Οι ιδιότητες του μεγέθους που τείνει στο συν ή πλην άπειρο με τις διάφορες πράξεις ορίζονται με βάση την κοινή λογική, όταν αυτό είναι εφικτό. Σε αυστηρή μαθηματική γλώσσα τα άπειρα μελετώνται με όρια, ενώ θεωρούνται προσεγγίσεις και όχι αριθμοί. Έτσι, ισχύουν οι εξής ιδιότητες (θ είναι ένας οποιοσδήποτε θετικός πραγματικός αριθμός):

Πρόσθεση και αφαίρεση

$+ \infty + θ = + \infty$
$- \infty + θ = - \infty$

$+ \infty - θ = + \infty$
$- \infty - θ = - \infty$ ^[1]

Πολλαπλασιασμός και διαίρεση

$+ \infty \cdot θ = + \infty$
$- \infty \cdot θ = - \infty$

$- \infty \cdot (- θ) = + \infty$
$+ \infty \cdot (- θ) = - \infty$

Παρομοίως με τη διαίρεση (γιατί 1/θ=η, όπου η ένας άλλος θετικός πραγματικός αριθμός)

Δυνάμη, ρίζα και λογάριθμος

$θ^{+ \infty} = + \infty$
$θ^{- \infty} = 0^{+}$

$(+ \infty)^{θ} = + \infty$
$(+ \infty)^{+ \infty} = + \infty$

$\sqrt[ν]{+ \infty} = + \infty$ , όπου ν φυσικός αριθμός
$\sqrt[+ \infty]{θ} = 1$

$l o g_{θ} (+ \infty) = + \infty, α ν θ > 1, - \infty, α ν 0 < θ < 1$

$l o g_{+ \infty} (θ) = 0$

0⁺, αν θ>1 και 0^- αν 0<α<1

Πράξεις με το μηδέν και το άπειρο

$+ \infty \pm 0 = + \infty$
$- \infty \pm 0 = - \infty$

$1 / 0^{+} = + \infty$
$1 / 0^{-} = - \infty$

$1 / \infty = 0$

Σειρές Taylor

Οι σειρές Taylor ορίζονται σε απείρως παραγωγίσιμες συναρτήσεις. Για τις σειρές Maclaurin χρειάζεται επιπλέον να ορίζονται στο 0.

Σειρές Maclaurin:

Γενικός τύπος: $f (x) = f (0) + f^{'} (0) \frac{x}{1} + f^{″} (0) \frac{x^{2}}{2!} + f^{3} (0) \frac{x^{3}}{3!} + . . . + f^{k} (0) \frac{x^{k}}{k!} + . . . = \sum_{n = 1}^{\infty} (f^{(n)} (0) \frac{x^{n}}{n!}) + 1$

Οι σειρά Maclaurin κάθε πολυωνυμικής συνάρτησης ισούται με την ίδια τη συνάρτηση.

$a^{x} = 1 + l n a \frac{x}{1} + l n a^{2} \frac{x^{2}}{2!} + l n a^{3} \frac{x^{3}}{3!} + . . . + l n a^{k} \frac{x^{k}}{k!} + . . . = \sum_{n = 1}^{\infty} (l n a^{n} \frac{x^{n}}{n!}) + 1$

$s i n x = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + . . .$

Βασικό τυπολόγιο παραγώγων πραγματικών συναρτήσεων πραγματικής μεταβλητής

Οι παρακάτω τύποι ισχύουν υπό την προϋπόθεση ότι τα σύμβολα έχουν νόημα, δηλαδή αν υπάρχουν οι παράγωγοι που εμφανίζονται. Το x είναι η ανεξαρτητη μεταβλητή και a είναι μια μη μηδενική σταθερά.

Βασικές παράγωγοι ως προς x:

$\frac{d a}{d x} = 0$	$\frac{d \ln x}{d x} = \frac{1}{x}$
$\frac{d x}{d x} = 1$	$\frac{d \sin x}{d x} = \cos x$
$\frac{d x^{a}}{d x} = a \cdot x^{a - 1}$ (εννοείται x $\neq$ 0,1)	$\frac{d \cos x}{d x} = - \sin x$
$\frac{d e^{x}}{d x} = e^{x}$	$\frac{d t a n x}{d x} = \frac{1}{c o s^{2} x}$

Κανόνες παραγώγισης:

$\frac{d (a f (x))}{d x} = a \frac{d f (x)}{d x}$
$\frac{d (f (x) + g (x))}{d x} = \frac{d f (x)}{d x} + \frac{d g (x)}{d x}$ ¹
$\frac{d (f (x) \cdot g (x))}{d x} = \frac{d f (x)}{d x} \cdot g (x) + f (x) \frac{d g (x)}{d x}$
$\frac{d \frac{f (x)}{g (x)}}{d x} =$ $\frac{\frac{d f (x)}{d x} \cdot g (x) - f (x) \cdot \frac{d g (x)}{d x}}{g^{2} (x)}$ ²
$\frac{d (g (f (x)))}{d x} = \frac{d g (f (x))}{d 𝐟 (𝐱)} \cdot \frac{d f (x)}{d x}$ (κανόνας της αλυσίδας)³

Πρότυπο:Σημείωση ¹:Ισχύει επαγωγικά ο τύπος και για περισσότερους όρους της πρόσθεσης, δηλαδή $\frac{d (f_{1} (x) + f_{2} (x) + \dots + f_{ν} (x))}{d x} = \frac{d f_{1} (x)}{d x} + \frac{d f_{2} (x)}{d x} + \dots + \frac{d f_{ν} (x)}{d x}$
²: Ισχύει υπό την προϋπόθεση ότι g(x) διάφορο του μηδενός κοντά στο σημείο εύρεσης της παραγώγου.
³: Ισχύει μόνο αν η f δε γίνεται κάπου σταθερή (σύμφωνα με το σχολικό βιβλίο μαθηματικών της Γ΄Λυκείου). Αν στην περιοχή εύρεσης της παραγώου η f είναι σταθερή, τότε η παράγωγος ισούται με 0 κοντά στο σημείο εύρεσης της παραγώγου. Εξ' άλλου η g δε μεταβάλλεται σε κάποια περιοχή μόνο και μόνο αν df(x)=0 σε αυτήν την περιοχή, άρα δε μπορεί να εφαρμοστεί ο κανόνας.

Παραδείγματα εφαρμογής των κανόνων

$\frac{d α^{x}}{d x} = \frac{d (e^{l n a})^{x}}{d x} = \frac{d e^{l n a \cdot x}}{d x} = \frac{d e^{l n a \cdot x}}{d (l n a \cdot x)} \frac{d (l n a \cdot x)}{d x} = e^{l n a \cdot x} \cdot l n a = l n a \cdot a^{x}$
$\frac{d l n (a x)}{d x} = \frac{d l n (a x)}{d a x} \cdot \frac{d (a x)}{d x} = \frac{1}{(a x)} \cdot a \cdot \frac{d x}{d x} = \frac{1}{x}$

$\frac{d \sin (a \cdot x)}{d x} = \frac{d \sin (a \cdot x)}{d (a x)} \cdot \frac{d a x}{d x} = \cos (a \cdot x) \cdot a \cdot \frac{d x}{d x} = a \cos (a \cdot x)$

*Προσοχή: Οι δύο παραπάνω τύποι ισχύουν, γιατί η συνάρτηση f(x)=ax δεν είναι σταθερή σε κανένα σημείο, ως γνήσια μονότονη.

$\frac{d (9 x^{3} - 2 x^{2} + x - 10)}{d x} = \frac{d (9 x^{3})}{d x} + \frac{d (- 2 x^{2})}{d x} + \frac{d x}{d x} + \frac{d (- 10)}{d x} = 9 \frac{d x^{3}}{d x} - 2 \frac{d x^{2}}{d x} + 1 + 0 = 9 \cdot 3 x^{2} - 2 \cdot 2 x + 1 = 27 x^{2} - 4 x + 1$

Σημειώσεις

Πρότυπο:Παραπομπές

↑ Αυτές οι ιδιότητες επιβεβαιώνουν τη φιλοσοφική άποψη ότι το άπειρο είναι αμετάβλητο.

[1] Αυτές οι ιδιότητες επιβεβαιώνουν τη φιλοσοφική άποψη ότι το άπειρο είναι αμετάβλητο.

[1]

Μαθηματικά για όλους/Γενικό τυπολόγιο: Διαφορά μεταξύ των αναθεωρήσεων

Τελευταία αναθεώρηση της 15:10, 15 Νοεμβρίου 2020

Μαθηματικές σταθερές

Αξιοσημείωτες ταυτότητες

Αναπτύγματα δυνάμεων διωνύμων

Παραγοντοποιήσεις

Παραγοντοποιήσεις αθροισμάτων και διαφορών δυνάμεων

Γενίκευση παραγοντοποιήσεων αθροισμάτων και διαφορών δυνάμεων

Άλλες παραγοντοποιήσεις

Ο τύπος του Διωνύμου και οι Διωνυμικοί Συντελεστές

Το παραγοντικό

Ο τύπος του διωνύμου

Διωνυμικοί συντελεστές

Ιδιότητες των διωνυμικών συντελεστών

Επέκταση για δυνάμεις πολυωνύμων

Τύποι Κλασικής Γεωμετρίας

Γεωμετρικά σχήματα

Τρίγωνο

Ορθογώνιο παραλληλόγραμμο

Πλάγιο παραλληλόγραμμο

Ρόμβος

Τετράγωνο

Τραπέζιο

Κανονικό πολύγωνο

Κύκλος

Τριγωνομετρικοί τύποι

Σχέσεις μεταξύ τριγωνομετρικών αριθμών

Τιμές των τριγωνομετρικών συναρτήσεων διαφόρων γωνιών

Τύποι αναλυτικής γεωμετρίας

Βασικές σχέσεις

Πράξεις με το συν-πλην άπειρο

Πρόσθεση και αφαίρεση

Πολλαπλασιασμός και διαίρεση

Δυνάμη, ρίζα και λογάριθμος

Πράξεις με το μηδέν και το άπειρο

Σειρές Taylor

Σειρές Maclaurin:

Βασικό τυπολόγιο παραγώγων πραγματικών συναρτήσεων πραγματικής μεταβλητής

Παραδείγματα εφαρμογής των κανόνων

Σημειώσεις

Μενού πλοήγησης

Αναζήτηση